
“Compound interest is the Eighth Wonder of the World. He who understands it, earns it; he who doesn’t, pays it.”
Albert Einstein supposedly said that. Lots of quotes get attributed to him that he didn’t actually say, and this may be one of them; I personally don’t see the guy who imagined riding a light beam to figure out the Theory of Relativity waxing poetic about compound interest.
But even if Einstein really didn’t say compound interest was the Eighth Wonder of the World, it’s still a good point. Compound interest is pretty dang awesome. It’s a powerful concept — one that can mightily strengthen, or weaken, your finances. The man who understands it will have a tool to increase his net worth; the man who doesn’t will go through life stuck in a paycheck mentality.
My seven-year-old son recently opened up a savings account, and it offered me the chance to explain compound interest to him. It didn’t go well. It’s one of those financial concepts that’s so simple that you take it for granted. Consequently, when you’re forced to explain it to a child, you realize you don’t have as much of a grasp on it as you thought you did. Einstein also supposedly said, “If you can’t explain it to a six-year-old, you don’t understand it yourself.” Again, even if he didn’t say that, it’s a good point.
If your dad never sat you down to talk compound interest, you’re in luck; having honed my explanation on Gus, I’ll now pass it along to you.
What Is Compound Interest?
To understand compound interest, it’s useful to understand simple interest first.
Simple interest is calculated on the principal or the original amount of a deposit or loan. It’s really, well, simple to figure out.
Let’s say you take out a loan for $10,000 at a simple interest rate of 5%. The duration of the loan is four years.
To calculate the interest that’ll accumulate on the loan, you’d use the following formula:
Principal x interest rate x term of the loan
Plugging in our numbers, it would be:
$10,000 x .05 x 4 = $2,000
So that $10,000 loan will cost you $2,000 in simple interest.
Car loans, home mortgages, and student loans use simple interest. A loan you take from a family member or friend will likely use simple interest (if they charge you interest at all).
Now that you understand simple interest, we can move to compound interest.
Compound interest is calculated on the principal amount and — this is key — also on the accumulated interest of previous periods. It’s interest on interest.
Here’s what the compound interest formula looks like:
P (1 + r/n) (nt) – P
[P = Principal; r = annual interest rate in percentage terms; n = number of compounding periods for a year; t = number of years money is invested or borrowed]
Yeah, it looks confusing, but let’s plug in our numbers from the simple interest example to see what we’d pay if the interest was compounded.
So we got a $10,000 loan that compounds annually at 5%. The duration of the loan is 4 years. What would we pay in interest? Let’s look at the progression of the math:
$10,000 (1+.05/1)(1×4) – $10,000 →
$10,000 (1+.05/1)(4) – $10,000 →
$10,000 (1.21550625) – $10,000 →
$12,155.0625 – $10,000 = $2,155.06
So on a four-year loan that’s compounded annually, we’d pay $2,155.06 in compound interest. That’s $155.06 more than a loan issued on simple interest. Calculating interest on the interest already accrued on a principal can really add up. And add up fast as we’ll see in an example below.
If you’d rather not do the math yourself, there are plenty of compound interest calculators online.
Credit cards calculate balances on compound interest. Instead of compounding annually, credit card companies compound monthly. The high interest rates of credit cards coupled with their monthly compounding is why pretty much every single personal finance guru out there says “Don’t carry a balance on your credit cards!” You end up paying a lot for that extended credit. For example, a credit card balance of $10,000 carried at an interest rate of 20% (compounded monthly) would result in total compound interest of $2,193.91 over one year, or about $183 per month. Imagine what you could do with an extra $183 a month.
Compound interest can work in your favor, though. Big time. When you sock your money into a savings account, banks typically pay compound interest daily on the money you keep with them. Granted, the interest rate you get is pretty crappy — somewhere between .03% and 1% depending on the bank — but when you compound at that rate daily and you keep that money in there for a long time, things can add up.
If you invest in an index fund, you can leverage the power of compound interest by re-investing your earnings into buying more of the index fund which will allow you to earn even more, which you then re-invest, and so on and so forth.
Compounding Periods Have a Big Effect on Earnings
Looking at the compound interest formula, you’ll likely notice that the frequency of compounding periods can have a big effect on your earnings or how much you have to pay in interest. The more compounding periods, the more interest that is accrued. You’ll earn more in interest from a bank that compounds daily compared to a bank that only compounds monthly; you’ll pay more in interest on a loan that compounds monthly compared to one that compounds annually.
So when looking at interest rates for a savings account or loan, make sure to pay attention to how often interest is compounded.
Time Is Your Friend
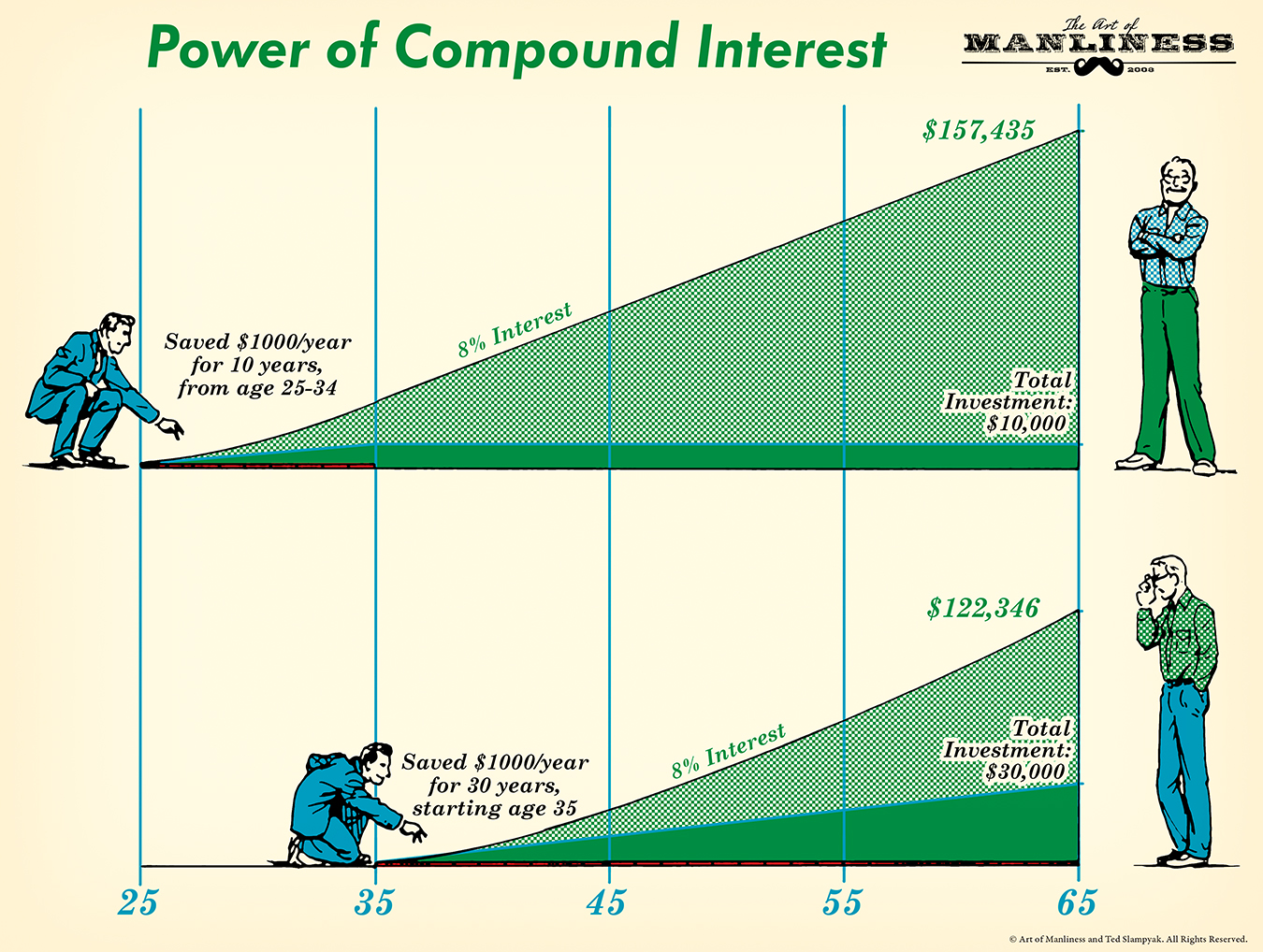
The real magic of compounding reveals itself over long periods of time. The longer you let your money sit in an account and compound itself, the more money you make.
This is the big point I’ve been trying to make to my son. What’s helped flip on the light bulb in his head is this example from personal finance expert Beth Kobliner:
If you were to save $1,000 a year from age 25 to 34 in a retirement account earning 8% a year, and never invest a penny more, your $10,000 investment would grow to $157,435 by age 65. But if you don’t start saving until you’re 35 years old and then invest $1,000 a year for the next 30 years (that’s a total investment of $30,000), you’ll have only $122,346 by age 65. The bottom line: Start early, so your money has enough time to pile up.
Understanding this concept has helped turn Gus into a tightfisted Scrooge McDuck. “Man, imagine how much interest I can earn since I’m starting at seven years old!” At the beginning of each month, he loves to check his savings account to see how the interest he earns is going up little by little thanks to the magic of compound interest.
Use the Power of Compound Interest to Your Advantage
Understanding compound interest can really help you move ahead with your personal finances. Knowing that credit card companies compound the interest on your balance on a monthly basis should act as an incentive to pay off credit card debt as quickly as possible. Knowing that you can make money from your money should act as an incentive to sock away as much dough as you can and to not touch it for as long as you can.
The key is to get started today. If you’ve got credit card debt, start paying it off now so compound interest doesn’t devour you. If you don’t have a savings or retirement account, start one today so you can leverage the power of this Eighth Wonder of the World.
Now that we have a basic understanding of compound interest, we can start exploring things like APR and APY. We’ll do that in a future article.
The post What Every Young Man Should Understand About the Power of Compound Interest appeared first on The Art of Manliness.
(via The Art of Manliness)






